The main idea of Proximal Method is to do gradient descent on $f$ with some "damping", even when the gradient does not exist. It is suitable for getting a "good-enough" answer for large data.
Definition
Definition Let $f$ be a convex function (with nonempty close convex epigraph). The proximal operator of $f$ is
$$\Mr{prox}_f(v) = \argmin_x\nail{f(x) + \frac{1}{2}\norm{x-v}_2^2}$$More generally, we can scale the regularization term:
$$\Mr{prox}_{\lambda f}(v) = \argmin_x\nail{f(x) + \frac{1}{2\lambda}\norm{x-v}_2^2}$$Interestingly, $\Mr{prox}_{\lambda f}(v)$ is defined everywhere, even when $v$ is not in the domain of $f$.
Example $f(x) = \norm{x}_1$ has proximal
$$\Mr{prox}_{\lambda f}(v) = \cases{ v-\lambda & \cif v-\lambda > 0 \\ v+\lambda & \cif v+\lambda < 0 \\ 0 & \cotherw }$$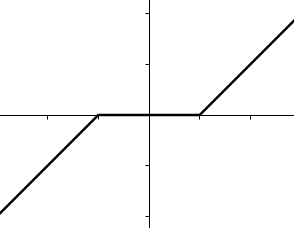
Interpretations
Generalized Gradient Descent
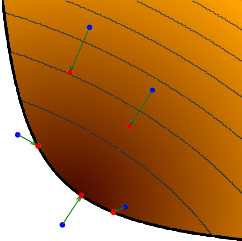
The colored area is the domain of $f$ (darker = lower), the blue points are $v$, and the red points are $\Mr{prox}_f(v)$. Suppose we move from $v$ to $\Mr{prox}_f(v)$:
- Points inside the domain moves to a lower point. Intuitively, $\Mr{prox}_f(v)$ is the middle ground between minimizing $f$ and being near $v$.
- Points outside the domain moves to the boundary of $f$.
Generalized Projection
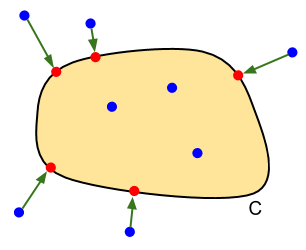
If $C$ is a convex set and
$$f = \II_C = \cases{0 &\cif x\in C \\ \infty &\cotherw}$$then the proximal of $f$ is the projection onto $C$:
$$\Mr{prox}_f(v) = \Pi_C(v) = \argmin_{x\in C}\norm{x-v}_2^2$$Properties
- (Separability)$$f(x,y) = \phi(x) + \psi(y) \quad\Rightarrow\quad \Mr{prox}_f(v,w) = \nail{\Mr{prox}_\phi(v), \Mr{prox}_\psi(w)}$$ However, $f(x,y) = f_1(x,y) + f_2(x,y)$ cannot be separated.
- (Post-composition)$$f(x) = a\phi(x) + b \quad\Rightarrow\quad \Mr{prox}_{\lambda f}(v) = \Mr{prox}_{(a\lambda)\phi}(v)$$
- (Pre-composition) -- not that important$$f(x) = \phi(ax + b) \quad\Rightarrow\quad \Mr{prox}_{\lambda f}(v) = \frac{1}{a}\nail{\Mr{prox}_{(a^2\lambda)\phi}(ax + b) - b}$$
- (Affine transformation)$$f(x) = \phi(x) + a\T x + b \quad\Rightarrow\quad \Mr{prox}_{\lambda f}(v) = \Mr{prox}_{\lambda \phi}(v - \lambda a)$$
- (Standard regularization)$$f(x) = \phi(x) + \frac{\rho}{2}(x-a)^2 \quad\Rightarrow\quad \Mr{prox}_{\lambda f}(v) = \Mr{prox}_{\lambda \phi}\nail{\frac{\tilde{\lambda}}{\lambda}v + p\tilde{\lambda}a}$$ where $\tilde{\lambda} = \lambda/(1+\rho\lambda)$
Conclusion If we know $\phi(x)$ and $\Mr{prox}_{\lambda \phi}$, we can do stuff with $\phi$ (like regularizing it) and still know the proximal.
Proximal Gradient Method
Because proximal is similar to gradient descent, we can minimize a convex function $f$ using the update rule
$$x^{(k+1)} \gets \Mr{prox}_f(x^{(k)})$$Example Suppose we want to minimize $f(x) + g(x)$ where $f$ is smooth but $g$ is not smooth (e.g., L1 regularization or encoded constraints). If we try to do gradient descent, we get
$$x^{(k+1)} \gets x^{(k)} - \eta_k\nabla f(x^{(k)}) - \eta_k\nabla g(x^{(k)})$$The problem is that $\nabla g(x^{(k)})$ does not exist. So we instead use the proximal update:
$$x^{(k+1)} \gets \Mr{prox}_{\eta_k g}\crab{x^{(k)} - \eta_k\nabla f(x^{(k)})}$$Basically, we converted $- \eta_k\nabla g(x^{(k)})$ to the proximal operator.
Example Let $f(x) = \frac{1}{2}x\T A x - b\T x$ where $A$ is positive definite. We know from calculus that $\argmin f(x)$ can be found by solving $Ax = b$. We can use proximal gradient method to get an iterative algorithm:
$$\begin{aligned} \Mr{prox}_{\lambda f}(v) &= \argmin_x \crab{\frac{1}{2}x\T A x - b\T x + \frac{1}{2\lambda}\norm{x-v}_2^2} \\ &= \text{... calculus ...} \\ &= v + (A + \epsilon I)^{-1} (b - Av) \end{aligned}$$where $\epsilon = 1/\lambda$. The update rule is
$$x^{(k+1)} \gets x^{(k)} + (A + \epsilon I)^{-1} (b - Ax^{(k)})$$The update rule above is called iterative refinement, which is particularly useful when $A$ is singular.
Alternating Direction Method of Multipliers (ADMM)
Setup Suppose we want to minimize $f(x) + g(x)$ where both $f$ and $g$ are not smooth. (Additionally, domains of $f$ and $g$ don't have to be the same!) Then the alternating direction method of multipliers (ADMM) is the following iterative update rules:
$$\begin{aligned} x^{(k+1)} &\gets \Mr{prox}_{\lambda f}(z^{(k)} - u^{(k)}) \\ z^{(k+1)} &\gets \Mr{prox}_{\lambda g}(x^{(k+1)} + u^{(k)}) \\ u^{(k+1)} &\gets u^{(k)} + (x^{(k+1)} - z^{(k+1)}) \end{aligned}$$The variables $x \in \operatorname{dom} f$ and $z \in \operatorname{dom} g$ converge to the same optimal value, while $u$ acts as a controller.
Special Case When $g = \II_C$ ($\Mr{prox}_g(v) = \Pi_C(v)$), ADMM is solving an optimization problem with convex constraint.
Theory
Theorem $x^*$ minimizes $f$ if and only if $x^* = \Mr{prox}_f(x^*)$
Proof ($\Rightarrow$) For all $x$,
$$\begin{aligned} f(x^*) &\leq f(x) \\ \underbrace{\frac{1}{2}\norm{x^* - x^*}_2^2}_{=0} + f(x^*) &\leq f(x) + \underbrace{\frac{1}{2}\norm{x - x^*}_2^2}_{\geq 0} \end{aligned}$$Therefore, by definition, $x^* = \Mr{prox}_f(x^*)$.
($\Leftarrow$) We use the following property of subdifferential (non-smooth generalization of derivative on convex functions):
$$\tilde{x} \text{ minimizes } g(x) \Leftrightarrow 0 \in \partial g(\tilde{x})$$Let $g$ be the thing in the definition of proximal:
$$\tilde{x} \text{ minimizes } \crab{f(x) + \frac{1}{2}\norm{x - v}_2^2} \Leftrightarrow 0 \in \partial f(\tilde{x}) + (\tilde{x} - v)$$Substitute $\tilde{x} = v = x^*$. We get $0 \in \partial f(x^*)$, meaning $x^*$ minimizes $f$. □