Problem Statement

Origin Q.E.D. Volume 38 Part 2 「十七」.

Here's a quote near the end of the chapter (no spoilers).

$Japanese version$

In 1796, when the great mathematician Gauss was 18 years old, he discovered that a regular 17-gon can be drawn using only a ruler and compass.

My friend Suthee posted the Thai version on Facebook:

$Thai version$

The ambiguous コンパス (compass) was translated as เข็มทิศ (navigational compass), which is different from วงเวียน (the tool for drawing circles).

That's a bad translation, but can we actually draw a regular 17-gon with a markless straightedge and a navigational compass? Assume that the compass is a perfect circle of unknown center and radius with a needle that always points north. You can place the compass so that its edge passes through 0, 1, or 2 points, trace its edge, and mark the point on the circumference where the needle points to.

$How the compass works$

Solution

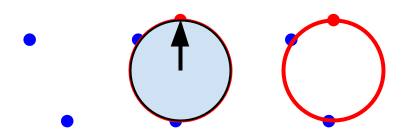
$Solution$

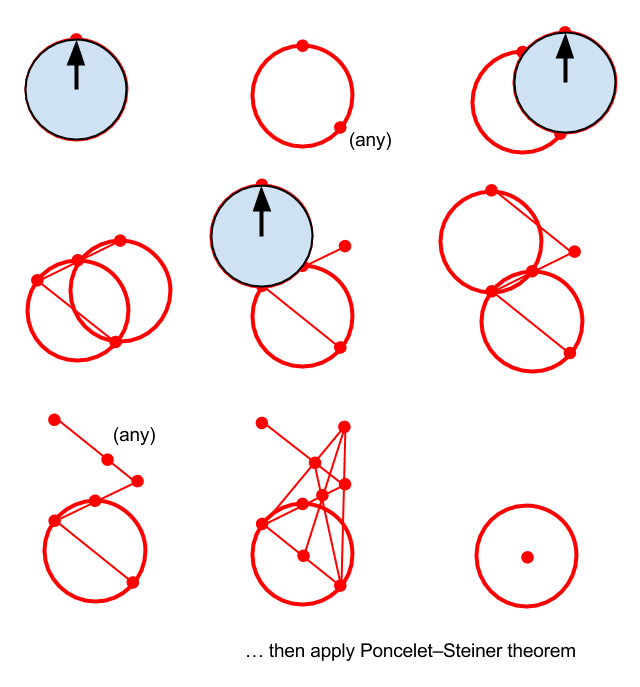
Poncelet-Steiner theorem: Whatever can be constructed by straightedge and compass can be constructed by straightedge alone if a circle and its center are given.

There should be a simpler solution, but this is the first one I could think of.